In probability theory the Chi-Square Distribution with n degrees of freedom is the distribution of a sum of the squares of n independent standard normal random variables defined as variable x
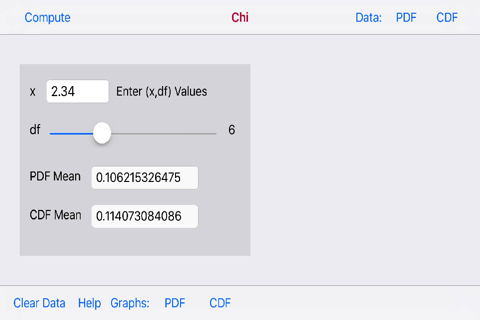
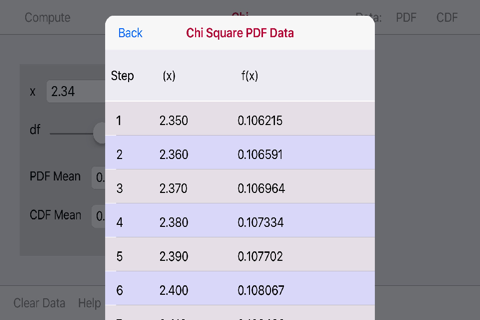
Chi-Square Distribution Integral Calculator calculates a table of (x,n)/F(x) value pairs from an interactive input of (x,n) and increment variables.
Arguments for the Chi-Square Distribution Integral.
x: The upper limit of the integral of the density function.
n: The number of degrees of freedom.
The (n) argument has a slider method of data input with a range of 1-20 degrees of freedom (df).
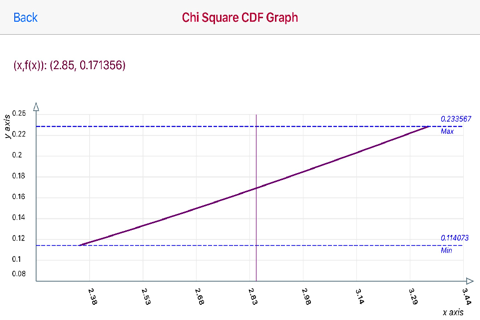
Chi-Square Distribution Integral Calculator also displays a graph for the (x,n)/F(x) generated values
The graphs are touch enabled graph. Upon touching the graph a vertical line appears. Move the vertical line to the left or right to display the point Pr(x) and the Chi Square Distribution PDF and CDF data pairs.
The horizontal x-axis displays x values. The vertical y-axis plots a range of either the CDF and PDF values
Horizontal Max and Min dashed lines display the Maximum and Minimum values.